| Nom du projet | Spatio-Temporal Modeling of Road Traffic in Urban Environment |
| Période | 2016 – 2019 / 2020 – |
| Financement | Contrat doctoral / Stage ENSMR |
| Rôle | Encadrement du doctorant Kamal Deep Oberoi (Directeur de thèse Pascal Vasseur, encadrant Yohan Dupuis) / Encadrement de stagiaires M2 : Mohamed Bakali el Mohamadi & Youssef el Kinany |
| Mots-clés | Modélisation de l’information spatiale et temporelle, multi-échelles, théorie des graphes, extraction de pattern temporel, analyse du trafic routier, mobilité |
| Site(s) web(s) | https://tel.archives-ouvertes.fr/tel-02438498 |
 
|
|
Contexte des travaux
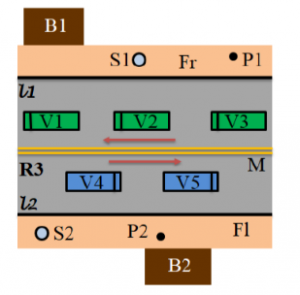
L’étude et l’analyse du trafic routier se fait souvent au travers d’indicateurs quantitatifs (e.g. densité, flux) calculés à partir de divers capteurs permettant de récupérer un certain nombre d’information comme la vitesse ou la géolocalisation par exemple. L’objectif de ces travaux est de proposer une modélisation qui introduit des aspects qualitatifs de l’information ce qui permettra d’obtenir des indicateurs complémentaires de ceux habituellement proposés.
Contribution
En terme d’extraction d’information, ce qui nous intéresse particulièrement est la possibilité de retrouver dans les données des situations particulières du trafic. A terme il s’agira par exemple de détecter des situations dangereuses ou interdites. Pour ce premier travail nous avons choisi trois exemples simples, et notre objectif est de produire un modèle et un algorithme permettant de retrouver ces situations (appelées « patterns » dans la suite du texte).
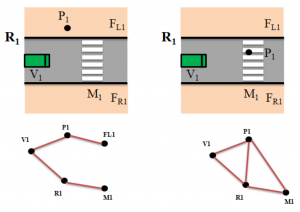
 Pattern 1 : sur 2 temps (t1-t2), le piéton P1 traverse sur le marquage M1, la rue R1 devant la voiture V1 |
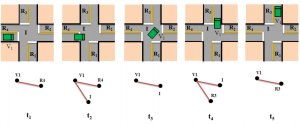
Pattern 2 : sur 5 temps, la voiture V1 tourne à l’intersection I de R4 vers R3 |
Pattern 3 : sur 5 temps, la voiture V1 tourne à droite sur R2, un piéton P1 traverse sur le marquage M1, la rue R2 (obligeant V1 à s’arrêter) |
Il faut imaginer un flot de données très conséquent sur une ville ou plus raisonnablement un quartier, voire une section de route particulière. Autrement dit, l’analyse doit être possible à plusieurs niveaux d’échelles.
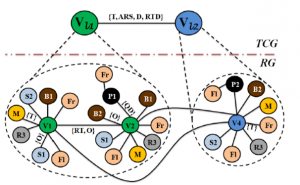
La modélisation choisie pour ce problème est un graphe spatialisés dans lequel chaque objet de l’environnement est un nœud et où l’on précise les relations spatiales entre ces objets au travers des arcs. Dans un premier temps on se contente de mettre une arête dès lors qu’il y a une relation spatiale entre deux objets de l’environnement, ce qui produit ces séquences de graphes associées à chacun des patterns.
 |
 |
 |
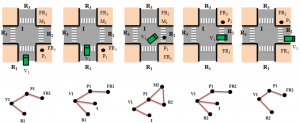Notons que c’est ici principalement la structure des graphes qui nous permet de différencier deux patterns différents. Les travaux de thèse qui ont été menés ont permis :
- De proposer un modèle formel permettant de définir la structure du graphe spatial et d’introduire la dimension temporelle afin de modéliser le trafic routier et son environnement.
- De développer l’algorithme basé sur la recherche d’isomorphisme de sous-graphes, qui permet de retrouver les patterns temporels dans la séquence de graphes représentant le flot de données relatif à la ville, au quartier ou à la section de route.
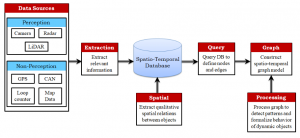
Ci-dessous un exemple de séquence de graphes représentant le flot de données relatif à une intersection. C’est par exemple dans cette séquence que l’on peut rechercher les différents patterns décrits plus haut.
Les travaux se poursuivent pour implémenter le workflow complet (ci-dessous).
Publications associées :
K. S. Oberoi, G. Del Mondo, Y. Dupuis, and P. Vasseur, « Modeling Road Traffic Takes Time, » in 10th international conference on geographic information science (giscience 2018), Dagstuhl, Germany, 2018, p. 52:1–52:7.
K. S. Oberoi, G. Del Mondo, Y. Dupuis, and P. Vasseur, « Towards a qualitative spatial model for road traffic in urban environment, » in 2017 ieee 20th international conference on intelligent transportation systems (itsc), 2017, pp. 1724-1729.
K. S. Oberoi, G. Del Mondo, Y. Dupuis, and P. Vasseur, « Spatial Modeling of Urban Road Traffic Using Graph Theory, » in Proceedings of Spatial Analysis and GEOmatics (SAGEO) 2017, Rouen, France, 2017, pp. 264-277.