| Nom du projet | Un modèle de graphe spatio-temporel pour représenter l’évolution d’entités géographiques |
| Période | 2008-2011 |
| Financement | Thèse |
| Rôle | Doctorante |
| Mots-clés | Modélisation de l’information spatiale et temporelle, théorie des graphes, multi-échelles, sciences de l’information géographique |
| Site web | https://tel.archives-ouvertes.fr/tel-00651682 |
| Principales collaborations | John G Stell (Univ. of Leeds) ; Andrea Rodriguez (Univ. of Concepcion) |
Travaux réalisés dans le cadre de ma thèse à l’Institut de Recherche de l’Ecole Navale (2008-2011), sous la direction de M. Christophe CLARAMUNT (PU) et de M. Rémy THIBAUD (MDC).
Les éléments contenus dans cette page ne visent pas l’exhaustivité, mais donnent une vue générale des travaux qui ont été réalisés.
Modélisation de l’évolution d’entités dans l’espace et le temps
Basée sur des notions de théorie des graphes et sur des travaux de [Stell2003], le modèle théorique sur lequel je travaille à pour vocation de représenter des entités de natures diverses (par exemple des dunes, mais aussi les parcelles d’un cadastre, des ronces, la généalogie de personnes, des phénomènes épidémiologiques etc.) afin d’en étudier l’évolution dans le temps et dans l’espace.
Les principes de base du modèle ont été publiés dans [Del Mondo & Al 2010] en collaboration avec le Dr J. G. Stell de l’université de Leeds en Grande Bretagne. Je présente ci-dessous un résumé du contenu de cet article.
La suite du travail s’est effectué en collaboration avec le Pr. A. Rodriguez de l’université de Concepcion au Chili, sur l’extension de ce modèle. En particulier, les extensions portent sur l’ajout de contraintes permettant l’adaptation de ce modèle très générique à divers types d’applications. L’article relatif à ces travaux a été publié dans la revue Data & Knowledge Engineering [Del Mondo & Al 2013].
Nous avons également poursuivi le travail avec le Dr J. G. Stell, mais cette fois pour une adaptation du modèle à la gestion de la granularité spatiale [Stell & Al 2011].
Enfin, en parallèle, nous avons travaillé en collaboration avec le Dr. A Mascret et le Service Hydrographique et Océanographique de la Marine (SHOM), sur une application du modèle à la problématique des dunes marines [Thibaud & Al 2013].
Principes de base du modèle de graphe spatio-temporel [Del Mondo & Al 2010]
Nous avons choisi de poser que chaque entité est associée à une région de R², mais notre modèle ne l’impose pas à priori.
Relations
Le modèle prend en compte trois types de relations :
- Relations spatiales
- Relations spatio-temporelles
- Relations de filiations
Relations spatiales
Il existe entre les entités une relation de connexion C qui peut être spécifiée comme relation du RCC8 [Cohn et al., 1997]. Le RCC8 comprend sept cas de connexion et un cas de déconnexion DC.
Relations spatio-temporelles
La relation spatio-temporelle est basée sur la relation spatiale mais entre des entités définis à des temps distincts. Soient les entités spatiales a et b existant respectivement au temps t et t0 avec t < t0. Si l’espace associé à l’entité spatiale b est en relation de connexion spatiale avec celui de a alors il existe une relation spatio-temporelle entre ces deux entités.
Relation de filiations
La relation de filiation est définie sur le concept de dépendance, qui est la transmission de l’identité lorsqu’une entité descend d’une autre. Nous distinguons deux types de filiations :
La filiation de type continuation : Si a et b entretiennent une relation de filiation de type continuation, cela signifie que a et b ont la même identité, il s’agit de la même entité mais à des temps différent.
La filiation de type dérivation : Si a et b entretiennent une relation de filiation de type dérivation, c’est à dire que b est une dérivation de a, c’est à dire que b est une dérivation de a (et potentiellement d’une autre entité s’il s’agit de relation parents-enfant). On considère qu’une partie de l’identité de a est présente dans b.

Exemple d’application à un cas « jouet » : la propagation des ronces
A titre d’illustration du modèle, nous avons proposé de modéliser l’évolution d’une population de ronces communes observée à quatre temps consécutifs.

Le graphe spatio-temporel associé est celui ci :

Chaque ronce est représentée dans le graphe par un nœud, et les relations spatiales et de filiations entre les ronces sont modélisées par les arêtes du graphe. L’empreinte spatiale d’une ronce est la projection de la plante sur le sol en prenant en compte à la fois les racines souterraines et les branches aériennes.
Les ronces possèdent quatre modes de propagation spatiale possibles, dont trois
cas de division et un cas de fusion : le marcottage, le drageonnage, la dispersion des graines et la greffe. On définit le sous-graphe permettant de caractériser chaque mode de propagation.
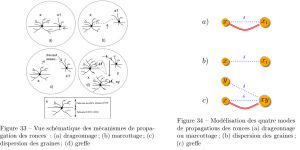
L’objectif est ensuite de les extraire du graphe représentant l’évolution des ronces.

Exemple d’application à un cas réel : l’évolution des dunes marines
L’étude de la dynamique des dunes sous-marines résulte entre autres de besoins en géosciences marines et relatifs à la sécurité de la navigation. Les données de dunes marines que nous avons utilisées ont été acquises dans la zone ci-dessous.
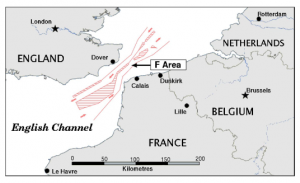
La figure ci-dessous représente les données bathymétriques d’un champ de dunes marines de cette zone entre les années 2002 et 2009.
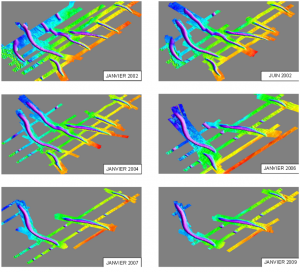
L’extraction des paramètres attributaires de ces dunes est effectuée à l’aide du logiciel ParamDune. Les 30 dunes identifiées sur les 6 enregistrements (de 2002 à 2009) ont été intégrées dans notre prototype. Dans un premier temps, ceci nous permet de valider l’intégration de données réelles dans ce prototype, ainsi que l’implémentation de ses différentes fonctionnalités.

Le graphe spatio-temporel ainsi défini, et une étroite coopération avec les experts du SHOM devait nous aider à caractériser la dynamique de ces dunes marines. D’un point de vue plus général, l’objectif est de pouvoir étudier des champs de dunes plus complexes. A ce stade de la collaboration avec le SHOM, l’utilisation de ces opérateurs pour l’analyse de processus n’a malheureusement pas été intégrée à ce travail.
Granularité spatiale et bigraphs
Des travaux plus exploratoires ont été menés sur la modélisation de la granularité spatiale. Le modèle qui en a découlé est indépendant du premier modèle de graphe spatio-temporel.
L’organisation hiérarchique des différents niveaux de détail dans la représentation de la granularité spatiale nous invite à utiliser ce type de structure. Il se trouve que les arbres d’inclusion sont utilisés dans une structure aux propriétés intéressantes au vu de notre modélisation spatio-temporelle : les bigraphs. Cette modélisation sous forme de bigraphs permet de conserver les liens de filiation entre les entités, de spécifier les modifications spatiales qui s’opèrent entre deux temps, et de représenter et de faire varier le niveau de granularité spatiale. Les relations spatiales entre entités autres que l’inclusion ne sont pas prévues au départ dans la définition des bigraphs, nous proposerons une piste pour
parer à ce problème. Le modèle basé sur les bigraphes repose sur la combinaison de deux graphes :
- un graphe de liens (relations de filiation) : un hypergraphe
- un graphe de places (relations spatiales) : une forêt
Un exemple de bigraph est proposé ci-dessous : Les entités Bi représentent des immeubles dans lesquels se trouvent des appartements (Fi). Dans ces appartements se trouvent des personnes (Pi ou Ei). Ei est potentiellement un enfant (ci) d’un Pi qui peut être son père (fi) ou sa mère (mi).

Nous avons cherché à introduire une dynamique à partir de cette modélisation à un temps donné, ce qui a conduit à l’émergence de règle de dynamiques, dont deux exemples sont présentés ci-dessous.

Publications associées
G. Del Mondo, A. M. Rodríguez, C. Claramunt, L. Bravo, and R. Thibaud, « Modeling consistency of spatio-temporal graphs, » Data knowl. eng., vol. 84, p. 59–80, 2013.
R. Thibaud, G. Del Mondo, T. Garlan, A. Mascret, and C. Carpentier, « A spatio-temporal graph model for marine dune dynamics analysis and representation, » Trans. GIS, vol. 17, iss. 5, p. 742–762, 2013.
G. Del Mondo, « Un modele de graphe spatio-temporel pour representer l’evolution d’entites geographiques. (A spatio-temporal graph-based model for the evolution of geographical entities), » PhD Thesis, 2011.
J. G. Stell, G. Del Mondo, R. Thibaud, and C. Claramunt, « Spatio-temporal evolution as bigraph dynamics, » in Spatial information theory – 10th international conference, COSIT 2011, belfast, me, usa, september 12-16, 2011. proceedings, 2011, p. 148–167.
G. Del Mondo, J. G. Stell, C. Claramunt, and R. Thibaud, « A graph model for spatio-temporal evolution, » J. UCS, vol. 16, iss. 11, p. 1452–1477, 2010.
