| Nom du projet | Étude des points fixes de la puissance de l’application de Kong – Ribenboim |
| Période | 2006 |
| Financement | Non financé |
| Rôle | Master 1 |
| Mots-clés | Ensembles partiellement ordonnés, antichaîne maximale, transformation ordre quelconque vers un ordre total |
 |
|
| Encadrant | Jean-Xavier Rampon (Univ. de Nantes) |
Ce travail est réalisé dans le cadre d’un travail d’encadrement et de recherche en 2006 sous la direction de M. J-X. Rampon. Notre principale référence est la C.R. A. S : “Chaining partially ordered sets” de Tat Yung Kong et Paulo Ribenboim.
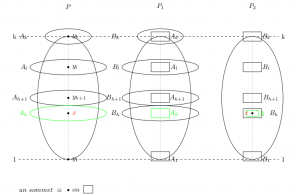
Nous commençons par rappeler quelques notions utiles à la compréhension du document. Ensuite nous présentons l’algorithme proposé dans la C. R. A. S. qui, appliqué à un ordre dont la hauteur est bornée par k, produit un ordre total (une chaîne) en au plus 2k – 1 itérations. Enfin, nous démontrons un certains nombre de propriétés afin de prouver l’existence de cette borne, et le nombre d’itérations m <= 2d(P)-1.
La section suivante est relative à un point particulier de l’étude dans le cas où l’on applique l’algorithme à un ordre infini. On cherche à quantifier le nombre d’antichaînes obtenues par un pas de l’algorithme qui peut être ‘beaucoup’ plus important que le nombre d’éléments de l’ordre initial, on le montre aussi dans le cadre d’un ordre fini.
Par la suite une autre partie propose une ébauche de recherche de cette borne sur des classes d’ordres particulières. Nous nous sommes intéressés à la classe des ordres série-parallèle et N-free.
Une dernière section est dédiée à la programmation en langage ISETL, le programme calcule la borne d’un ordre défini préalablement.
