| Nom du projet | Décomposition modulaire dans les réseaux métaboliques, extension avec la décomposition homogène |
| Période | 2007 |
| Financement | Non financé |
| Rôle | Master 2 recherche |
| Mots-clés | Décomposition modulaire, décomposition homogène, théorie des graphes, complexes macro-moléculaires, réseaux d’interaction de protéines (PPI) |
| Site web | https://academic.oup.com/bioinformatics/article/25/7/926/210962 |
  |
|
| Encadrants | Irena Rusu & Damien Eveillard (Univ. de Nantes) |
La théorie des graphes peut être appliquée dans de nombreux domaines et en particulier à la biologie.
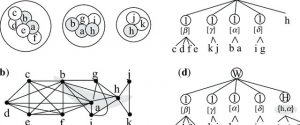
D’un point de vue théorique, la décomposition modulaire permet de trouver les différents modules d’un graphe. Un module d’un graphe G=(V,E) est un ensemble de sommets M inclut dans V tel que tous les voisins de M ont les mêmes voisins dans V – M. On peut dire que tous les sommets de M sont perçus comme un seul par l’ensemble des sommets de V – M.
Appliquée à un réseau métabolique, cette décomposition permettrai de trouver les unités fonctionnelles qui compose le réseau. Ces unités sont des entités semi-autonomes qui présentent des connections fonctionnelles denses avec les autres unités et plus lâches avec l’environnement.
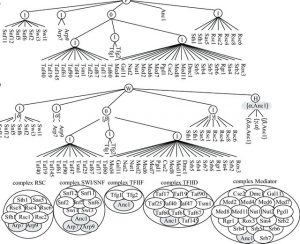
L’article de Julien Gagneur ‘Modular decomposition of protein-protein interaction networks’ (2004) illustre cette application.
Les travaux auxquels j’ai participé avec avec Mme Irena Rusu (PU) et M. Damien Eveillard (MCU) portent sur une extension de cette méthode, la décomposition homogène.
poster JOBIM
Publication associée :
G. Del Mondo, D. Eveillard, and I. Rusu, « Homogeneous decomposition of protein interaction networks: refining the description of intra-modular interactions, » Bioinformatics, vol. 25, iss. 7, p. 926–932, 2009.
